本文是谷歌机器学习速成课程的学习笔记。
简介
机器学习是人工智能的一个分支。机器学习是实现人工智能的一个途径,即以机器学习为手段解决人工智能中的问题。
机器学习有下面优势:
- 可以增加编程效率。比如可以快速开发拼写纠正程序,而不是通过研究语法来实现逻辑。
- 可以制作更通用的工具。如果已经使用机器学习编写了针对一种语言的拼写纠正程序,那么只要通过提供相应的数据就可以快速实现针对另一种语言的拼写纠正程序。
- 解决无法用常规的逻辑解决的问题。如果没有机器学习,你很难教机器如何识别一个苹果。
除了上述优势之外,学习机器学习还可以改变我们的思考方式:我们可以跳出原有的使用逻辑来实现功能的思维方式,利用机器学习去实现一些以前根本无法想象的功能。
术语
监督式机器学习(Supervised Learning)
監督式學習,是一個機器學習中的方法,可以由訓練資料中學到或建立一個模式(函數/ learning model),並依此模式推測新的实例。
如果想教会机器识别垃圾邮件,首先给机器提供大量邮件并且告诉机器:「这是垃圾邮件」或者「这不是垃圾邮件」。通过大量的「训练」之后,机器就可以预测一封从未见过的邮件是不是垃圾邮件。
标签(Label)
标签是我们需要机器判断的事物,是机器学习预测的答案或结果。如一封邮件「是不是垃圾邮件」。
特征(Feature)
特征是机器识别对象的某种性质,是机器学习预测的输入变量。如一封邮件的标题、发件人地址、包含某个特定短语。
样本(Example)
样本是数据的特定实例,如一封邮件。样本分为两类:
- 有标签样本:同时包含特征和标签,如一封垃圾邮件或一封正常邮件。
- 无标签样本:仅仅包含特征而没有标签,如一封邮件但我们并不知道是否是垃圾邮件。
我们通过有标签样本来训练我们的模型,然后使用训练好的模型来预测无标签样本的标签。
模型(Model)
模型定义特征与标签之间的关系。模型的生命周期分为两个阶段:
- 训练/学习:通过提供大量的样本,让模型学习特征与标签之间的关系。
- 推断:训练完毕后,模型便可以预测无标签样本的标签。
回归与分类
- 回归模型(regression model)用来预测连续值:如房价、点击概率。
- 分类模型(classification model)用来预测离散值:如判断邮件是不是垃圾邮件,图片中包含的内容是猫还是狗。
完整的术语列表。
线性回归(Linear Regression)
在某些情况下,特征和标签之间是简单的线性关系,如气温和蟋蟀鸣叫次数:
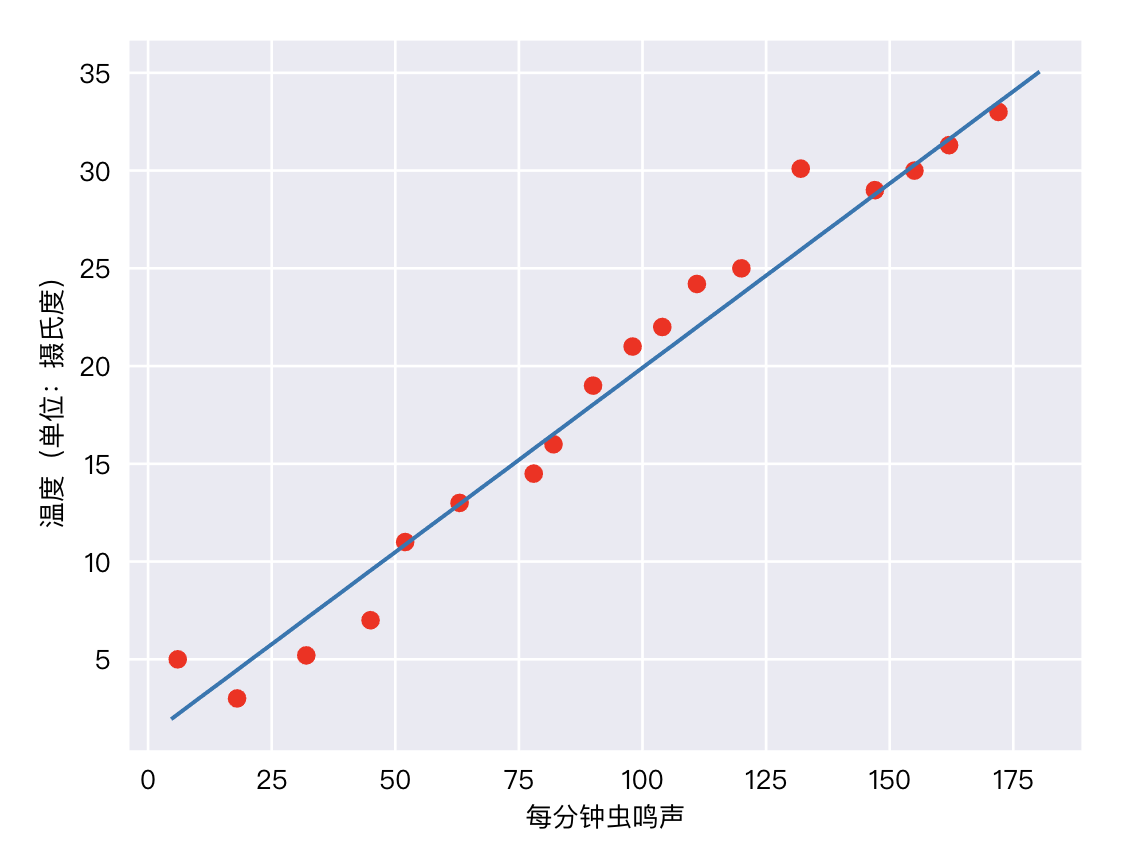
所谓线性关系,就是我们可以通过画一条直线来近似表示两者之间的关系。初中数学告诉我们,可以用下面的公司来表示:
$$y = mx + b$$
按照机器学习的惯例可以写成:
$$y’ = b + \omega_1x_1$$
其中
- $y’$ 是预测标签。
- $b$ 是偏差(y 轴截距)。
- $\omega_1$ 是特征1 的权重。
- $x_1$ 是特征值。
实际应用中一个模型可能包含多个特征:
$$y’ = b + \omega_1x_1 + \omega_2x_2 + \omega_3x_3$$
训练(Training)与损失(Loss)
在训练过程中,模型预测得出的值与实际值是有损失的。比如下面两个模型
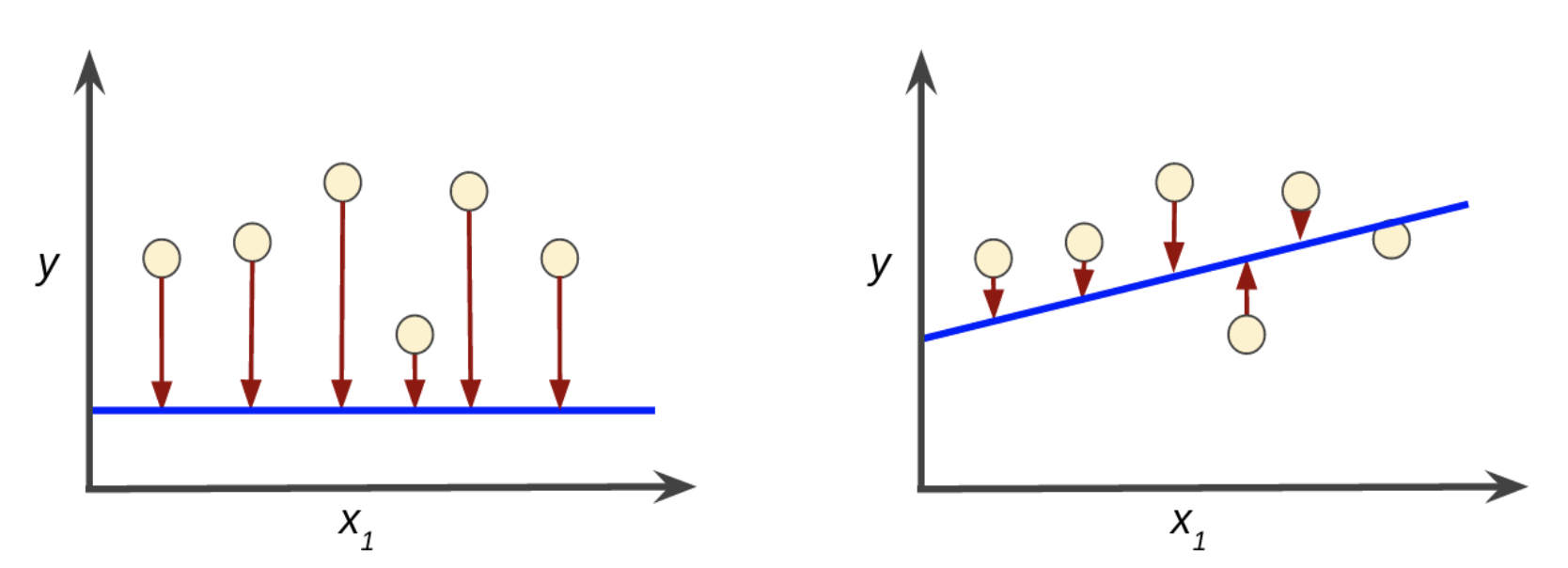
图中蓝线表示预测,红色箭头表示损失。不难看出左边的模型损失比较大,换句话说,右边的模型预测更准确。
如何衡量不同模型的准确程度?中学数学中有一个方差的概念:
$$MSE = \frac{1}{N}\sum_{(x,y) \in D} (y - prediction(x))^2$$
其中:
- $(x,y)$ 指的是样本,$x$ 是特征,$y$ 是标签。
- $prediction(x)$ 是模型预测的值。
- $D$ 是样本集。
- $N$ 是样本数量。
尽管方法是机器学习常用的损失函数,但它不是唯一、也不一定是所有情况下最好的损失函数。
降低损失
现在我们知道了我们的目标:使用模型通过特征来预测标签,也知道了完成目标的衡量标准:损失,接下来就是如何减少损失。
迭代方法
在机器学习中,一般通过迭代的方法来找到最佳模型。
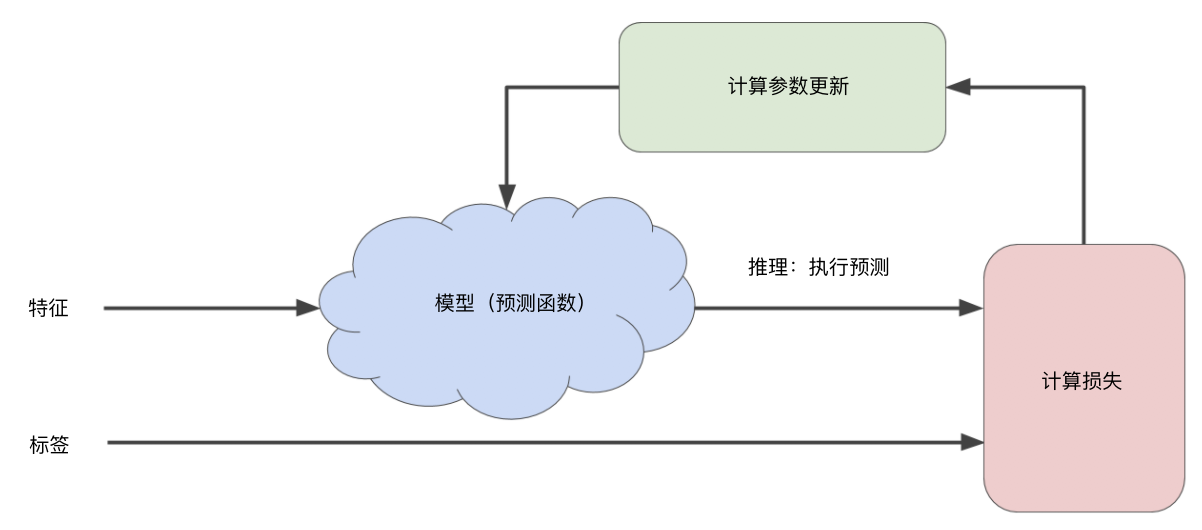
通过不断调整计算参数并计算新参数下模型的损失,最终找到一组使损失最小的参数。
比如前面的例子:
$$y’ = b + \omega_1x_1$$
我们需要确认的参数是 $b$ 和 $\omega_1$。于是机器学习系统会随机产生两个值带入进入,计算其损失值(比如使用前面提到的方差计算法),然后根据得出的损失值不断调整这两个参数代入模型,直到损失不再变化或者变化及其缓慢为止。这个时候可以说模型已经收敛。
因此最关键的部分是如何计算参数更新。
梯度下降法(Gradient Descent)
对于回归问题,所产生的损失与权重的图形始终是凸形。
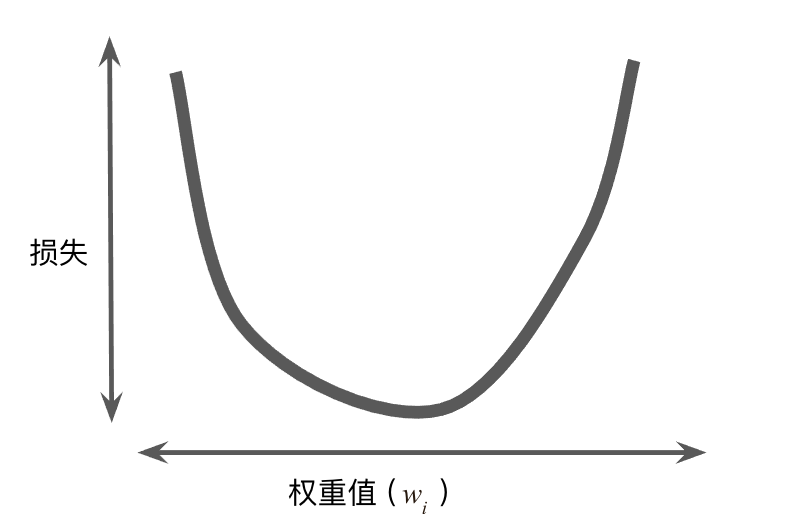
因此我们总是能找到一个 $\omega$ 使得损失最小。当然我们可以通过枚举所有的 $\omega$ 来找到使损失最小的值,但这样的计算代价往往不能接受。我们通常使用梯度下降法。
首先我们随机取一个起点,然后计算损失曲线在起点处的梯度。梯度是偏导数的矢量,指向损失函数增长最快的方向,那么沿着梯度相反的方向来调整权重就可以快速降低损失。
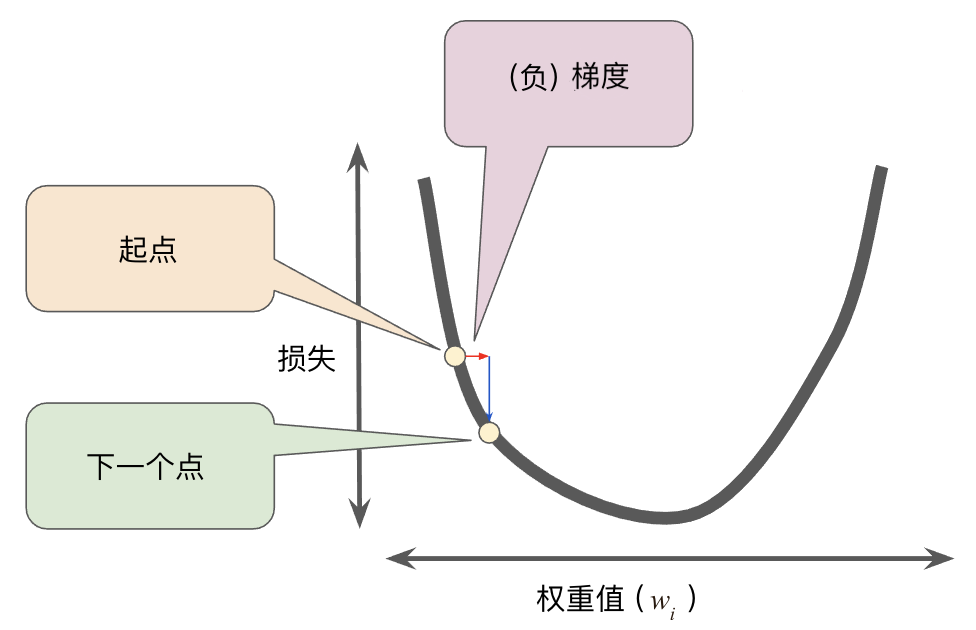
通过在起点上增加梯度调整到下一个点,然后一步一步逼近使损失的最小值。
学习速率(Learning Rate)
前面我们了解到,我们通过向梯度相反的方向来调整参数,其中调整速度的快慢被称作学习速率(也叫步长)。梯度是矢量,具有方向和大小,假设梯度的大小是 0.25,学习速率是 0.1,那么下一个参数的值就是当前的值加上 0.025。
学习速率过高或者过低都会有问题:
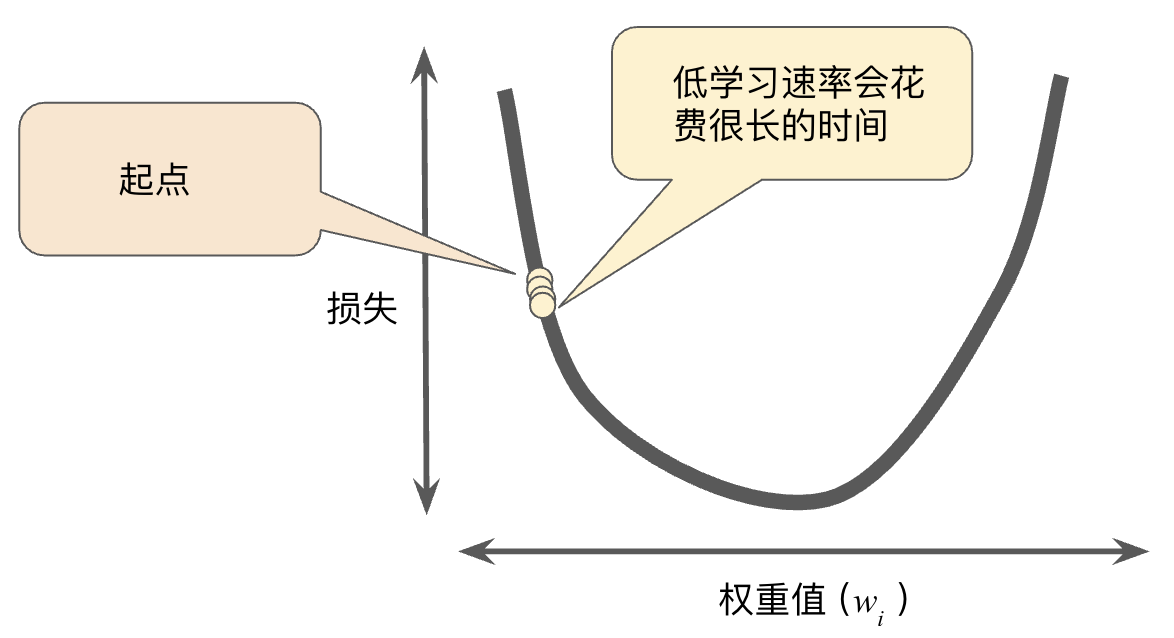
学习速率过低会大大增加计算量。
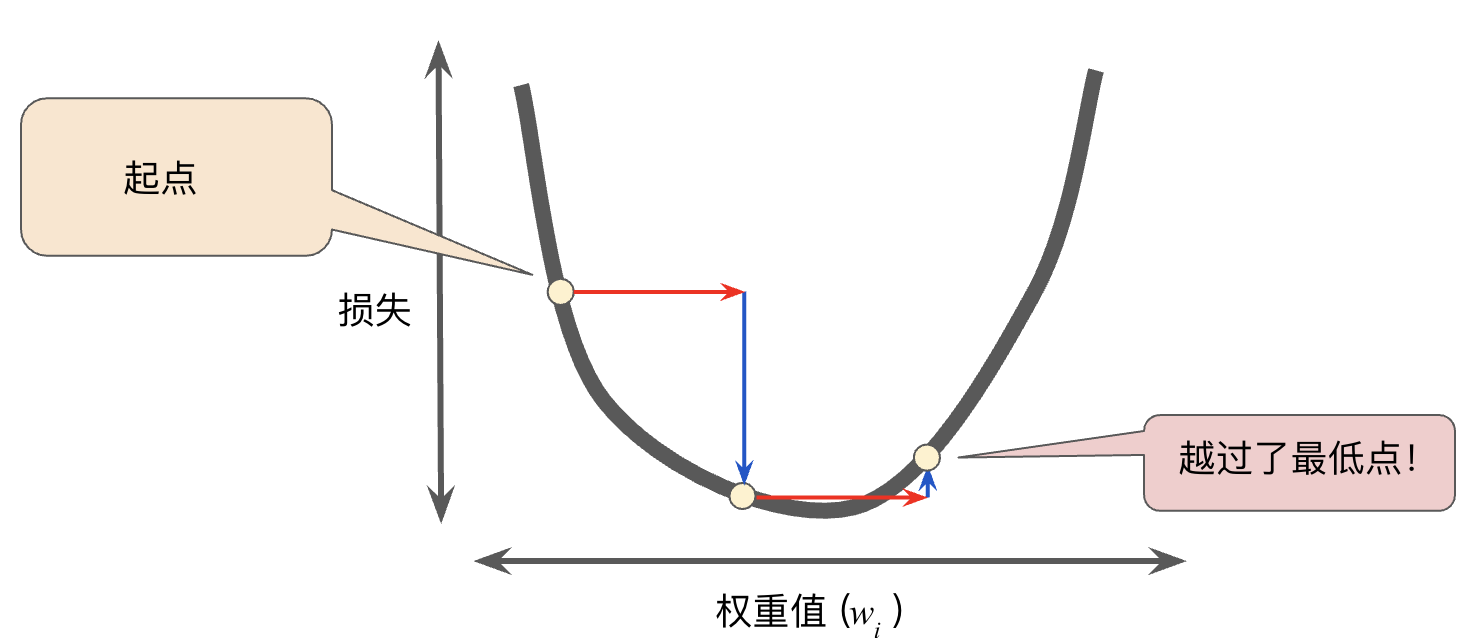
学习速率过高则有可能会错过最低点。
因此如何设置恰当的学习速率是非常关键的。这种用来调整机器学习算法的值被称作超参数(hyperparameter)。
随机梯度下降法
在梯度下降法中,批量指的是用于在单次迭代中计算梯度的样本总数。在每一次迭代中,我们对选择样本有三种策略:
- 批量梯度下降法(Batch Gradient Descent):每次迭代计算整个数据集的损失。这样做的好处是可以得到全局最优解,坏处是计算量非常大,并且因为超大批量的数据包含了大量冗余数据,使用起来并不一定比大批量数据好。
- 随机梯度下降法(Stochastic Gradient Descent):每次迭代只随机抽取一个样本(批量大小为 1)。显然这样做随机性太大,效果也不好。
- 小批量随机梯度下降法(Mini-batch Gradient Descent):介于前两者之间的方法,每次随机选取 100~1000 个样本。这样兼顾了效率和准确性。

